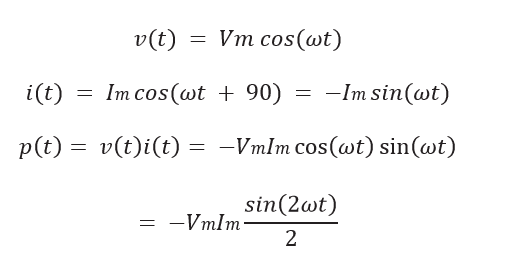Reactive Power:
Reactive power is an imaginary power which is delivered by capacitors and alternators. Consider the case in which the load is a pure capacitance for which Z =(1/ωC) ∠−90◦ . Then, θ= −90◦, and we have
[wp_ad_camp_1]
Here again, the average power is zero, and we say that reactive power flows. Notice, however, that the power for the capacitance carries the opposite sign as that for the inductance. Thus, we say that reactive power is positive for an inductance and is negative for a capacitance. If a load contains both inductance and capacitance with reactive powers of equal magnitude, the reactive powers cancel.
Power surges into and out of capacitances in ac circuits. The average power absorbed by capacitances is zero.
In ac circuits, energy flows into and out of energy storage elements (inductances and capacitances). For example, when the voltage magnitude across a capacitance is increasing, energy flows into it, and when the voltage magnitude decreases, energy flows out. Similarly, energy flows into an inductance when the current flowing through it increases in magnitude. Although instantaneous power can be very large, the net energy transferred per cycle is zero for either an ideal capacitance or inductance.
When a capacitance and an inductance are in parallel (or series) energy flows into one, while it flows out of the other. Thus, the power flow of a capacitance tends to cancel that of an inductance at each instant in time.
The peak instantaneous power associated with the energy storage elements contained in a general load is called reactive power and is given by
[wp_ad_camp_1]
where θ is the power angle or Power factor. Vrms is the effective (or rms) voltage across the load, and Irms is the effective current through the load. (Notice that if we had a purely resistive load, we would have θ = 0 and Q = 0.)
The physical units of reactive power are watts. However, to emphasize the fact The units of reactive power Q that Q does not represent the flow of net energy, its units are usually given as Volt are VARs. Amperes Reactive (VARs).
Importance of Reactive Power:
The power flow back and forth to inductances and capacitances is called reactive power. Reactive power flow is important because it causes power dissipation in the lines (power loss) and transformers of a power distribution system.
Even though no average power is consumed by a pure energy-storage element (inductance or capacitance), reactive power is still of concern to power-system engineers because transmission lines, transformers, fuses, and other elements must be capable of withstanding the current associated with reactive power. It is possible to have loads composed of energy-storage elements that draw large currents requiring heavy-duty wiring, even though little average power is consumed. Therefore, electric-power companies charge their industrial customers for reactive power (but at a lower rate) as well as for total energy delivered.