Kirchhoff’s Voltage Law Kirchhoff’s Current Law :
Kirchhoff’s Law is one of the Popular electrical and electronic circuit law next to ohm’s law. Every electrical and electronic student must know this law. These laws are invented by German physicist Gustav Robert Kirchhoff on 1824-1887. These are valid for the circuit’s components such as active components (current sources, voltage sources, and others) and passive components (resistor, inductor, capacitor, etc). Two of Kirchhoff’s laws are
- Kirchhoff’s Current Law.
- Kirchhoff’s Voltage law.
Let’s see the detailed explanation about Kirchhoff’s laws
Kirchhoff’s Current Law (KCL):
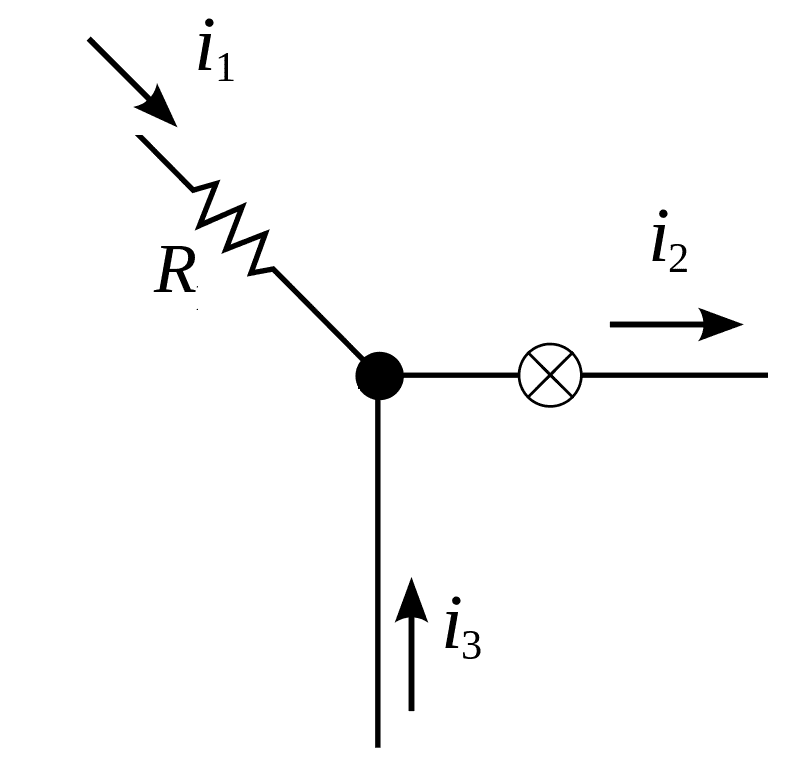
KVL states that algebraic sum of current in a junction point is equal to zero. Or the incoming current is equal to outgoing current or current entering in a node is equal to current leaving a node.
Let consider a network, which is having three resistor R1, R2 and R3, the current flowing through the resistors in the same order as I1, I2, and I3. Three resistors are joined at node A. In this circuit, current I1, I3 are entering into the node A and current I2 is leaving from node A. Hence the current entering the node I1 and I3 we should consider as the positive sign and Current I2 as the negative sign.
[wp_ad_camp_1]
Apply KCl to the network.
Key Points:
- The algebraic sum of current entering the node is equal to current leaving a node.
- Current entering will get + sign and the current leaving will get –ve sign
- If current source present in the same circuit means conventional current direction is considered as the reference direction
Simple Solution:
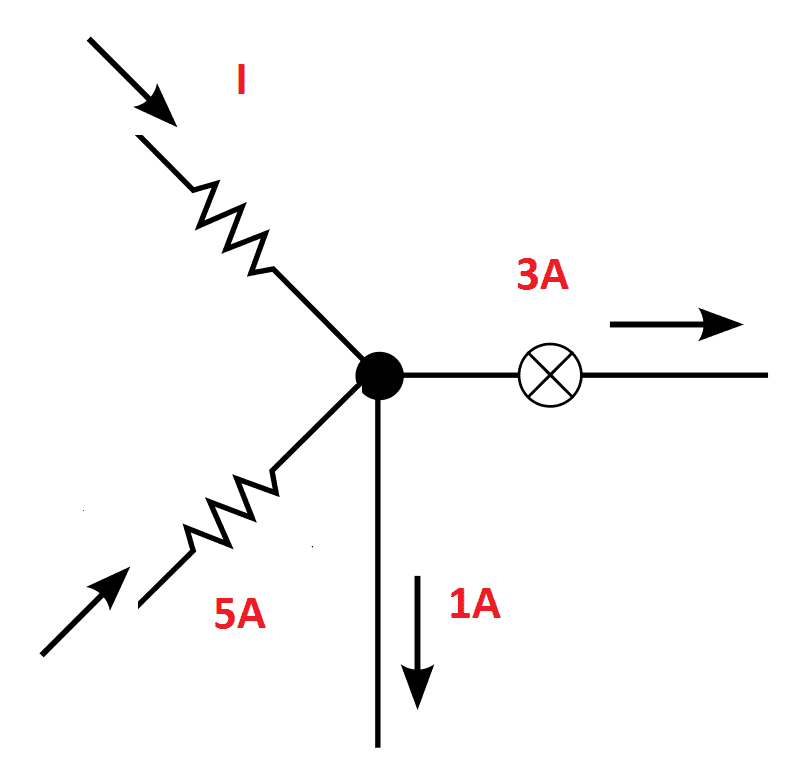
Solve the figure,
Unknown Current I and 5 Amps are entering the node the same get positive sign +I and +5 Amps, 1 Amps and 3 Amps are leaving from the node A and the same gets negative -1 and -3 Amps. Apply KCL to the Node A,
Kirchhoff’s Voltage law:
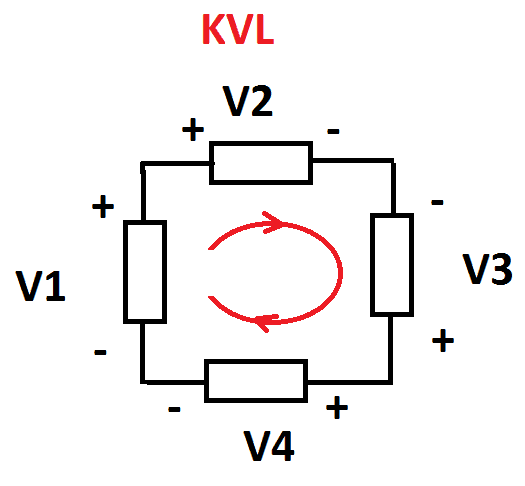
KVL stats the algebraic sum of voltages in the closed loop is equal to zero. Consider four voltage sources or four elements and the voltage across each element V1, V2, V3, and V4 are connected in the closed loop. Current I is the current flowing through the circuit. Please refer to the circuit diagram.
When I the current passes through an element from positive to negative the voltage across that element is a drop. When the current passes through an element from negative to positive, the voltage is a rise.
Also, we go around the loop, we pass each element of the circuit from +ve side of its voltage drop to negative side or negative side of its voltage rise to the positive side. Here we consider as the voltage rise as the +ve side and the voltage drop as –ve side of the circuit.
Note: Conventional current direction is taken as reference direction.
Apply KVL,
Key Points:
- Current I flow from Positive to the negative => Voltage drop
- Current I flow from Negative to Positive => Voltage rise.
- Sum of voltage drop is equal to voltage rises in the circuit
Example:
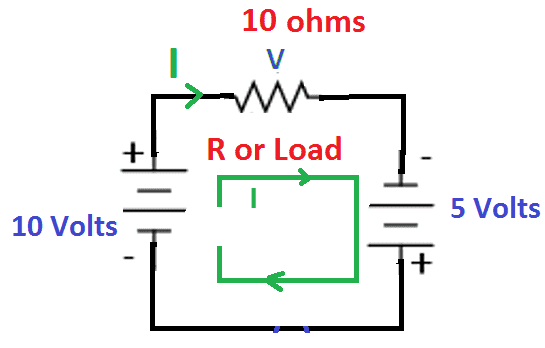
Find the current flowing through the resistor and voltage drop across the resistor.
[wp_ad_camp_1]
Solution:
I= current flowing in the circuit
V= Voltage across the resistor
In the above circuit, the current enters in the negative terminal and leaves positive terminal of the voltage source V1=10 V, then there is a voltage rise (positive sign). In second voltage source 5V and the resistor, current I enter into a positive terminal and leaves in negative terminal hence voltage drop across the terminal, both gets negative sign.
Apply KVL,
Hence the current through the circuit:

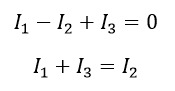
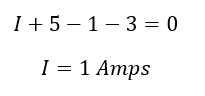
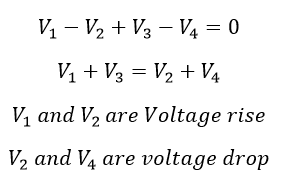
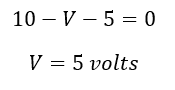
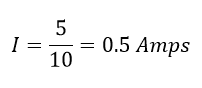











![What is Arc Chute? Types, Working Principle [Video Included] arc chute working priciple](https://www.electrical4u.net/wp-content/uploads/2020/06/arc-chute-218x150.png)