IDMT tripping time calculation:
Enter the TMS, Current setting and fault current, then press the calculate button to get the tripping time based on the relay characteristics setting.
IDMT Tripping Time Calculation:
Inverse Definite Minimum Time is a type of calculation which provides the relay tripping time varies to the fault current, which means when the fault current low means we get high tripping time and the relay operates by certain time meanwhile while the fault current is high means, the relay operates at less time.
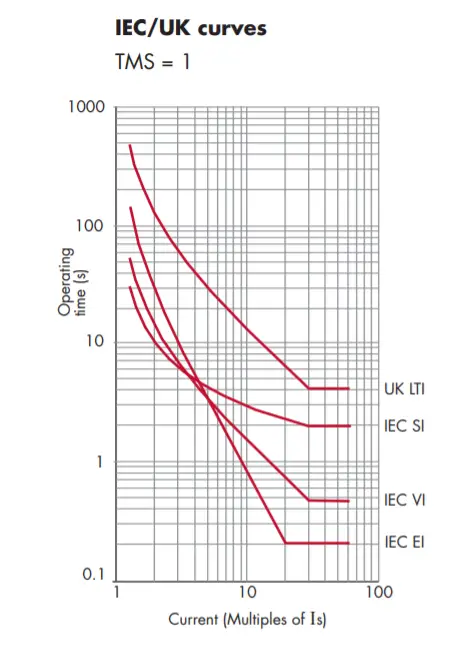
Basically, four types of relays are being manufactured based on their characteristics curve (Characteristics curve means the relay manufacture defines how the relay operates with respect to time). They are Standard inverse (LV), Very inverse (LV, MV), extreme inverse (LV,MV, HV and EHV), and longtime standard inverse (VLV, LV,MV, HV and EHV).
For your easy understanding, the relay sensitivity works such as
Extreme inverse > very Inverse > Standard Inverse > Long Time Standard Inverse.
Here, long time standard inverse consist of least sensitivity which often used as over load protection and the extreme inverse consist of higher sensitivity (Example: 110kV SF6).
For calculating IDMT tripping time, we have taken three standard such as IEC60255, IEEE, and US.
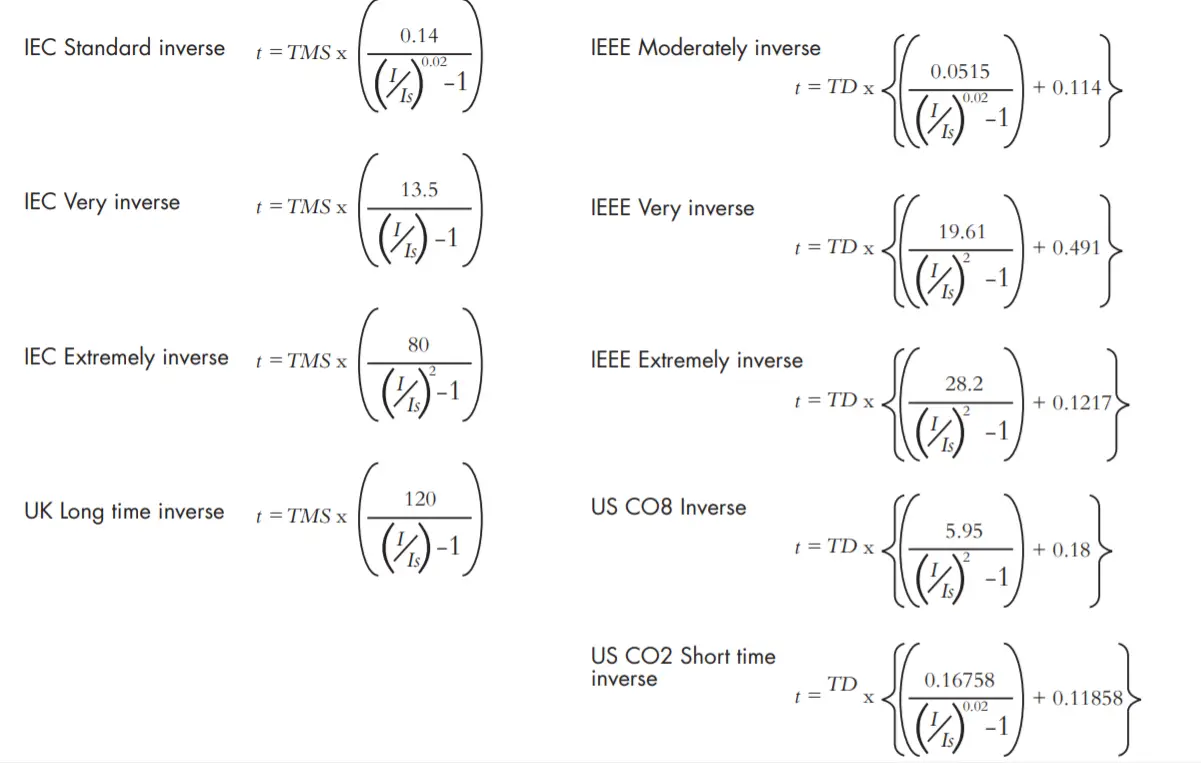
IDMT Calculation as per IEC:
Here, as defined in IEC 60255, the IDMT Tripping Time T(s) is multiplication of Time Setting Multiplier (TSM) by the k curve constant divided by the division of fault current I(F) in Amps to relay Current setting Is(A) in amps power of curve constant α minus 1.
Hence the formula can be written as,
T(s) = TSM * (k / ((I(F)/Is(A)) α – 1))
Here the curve constant k and α are given below and it will be varied based on the type of characteristics curves are used.
| IEC 62055 IDMT Curve Constant | ||
| Curve Type | α | k |
| Standard inverse | 0.02 | 0.14 |
| Long time standard inverse | 1 | 120 |
| Very inverse | 1 | 13.5 |
| Extremely inverse | 2 | 80 |
Look at the curve trip timing with various IF,
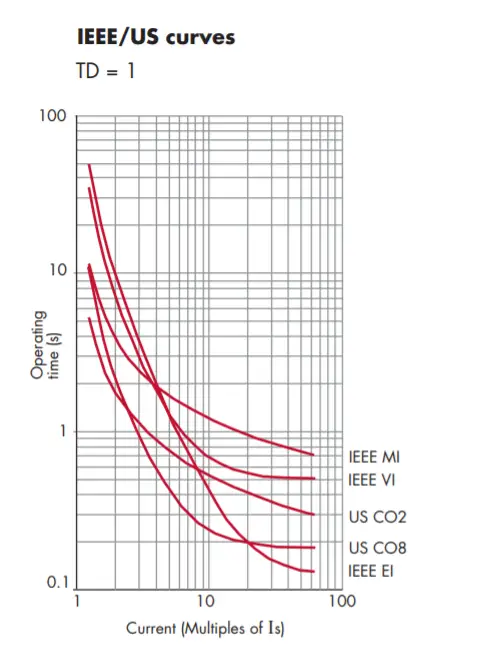
IEEE Standard IDMT Calculation:
Also, the IEEE section C37.112-1996 defines the IDMT timing in seconds by the below formula,
t(s) = TD/7 ((A / (I(F)/Is)p – 1) + B)
Normal range of TD is 0.5 to 15
Hence, the formula in terms of TSM,
T(s) = 0.143 * TSM * ((A / (I(F)/Is)p – 1) + B)
The IDMT is equal to 0.143 times of time setting multiplier TSM multiplication of sum of curve constant B and the ratio of curve constant A to the ratio of power of p of ratio of fault current IF to the relay current set value Is and minus 1
As we said above the A, B, p are the curve constant and IF = Actual Fault current in Amps and Is = Relay Setting current in Amps.
| IEEE Tripping Curves Constant | |||
| Curve type | p | A | B |
| Inverse | 0.02 | 0.0515 | 0.114 |
| Very inverse | 2 | 19.61 | 0.491 |
| Extremely inverse | 2 | 28.2 | 0.1217 |
IEEE Curve:
American standard IDMT relay tripping Calculation:
According to American standard the over current relay is classified based on the following,
- Definite minimum- CO-6.
- Moderately inverse – CO-7
- Inverse, CO-8.
- Very inverse – CO-9
- Extremely inverse – CO-11
The formula for co-8 inverse curve will be
t(s) = TD (0.18 + (5.95 / (I/Is)2 – 1))
The formula for co-6 inverse curve will be
t(s) = TD (0.11858 + (0.16758 / (I/Is)0.02 – 1))
IDMT Calculation Example:
Let us calculate the IDMT tripping time of the relay as per IEC standards which carries 8000A of fault current, and it have pickup current of 800 A. And the time dial is 1, calculate the IDMT for the different standard such as IEC, IEEE, and NEC.
From Above,
Relay Pickup Current: 800 (A)
Fault Current: 8000 (A)
Time Multiplier Setting: 1
Standard Inverse:
Tripping Time: 2.97060 (S)
Tip Curve: IEC 60255 Very Inverse
Tripping Time: 1.50000 (S).
Tip Curve: IEC 60255 Extremely Inverse:
Tripping Time: 0.80808 (S)
Tip Curve: IEC 60255 Long-Time Inverse:
Tripping Time: 13.33333 (S)
Tip Curve: IEEE Moderately Inverse:
Tripping Time: 0.17257 (S)
Tip Curve: IEEE Very Inverse:
Tripping Time: 0.09854 (S)
Tip Curve: IEEE Extremely Inverse:
Tripping Time: 0.05814 (S)
Tip Curve: US CO8 Inverse:
Tripping Time: 0.03433 (S)
Tip Curve: US CO2 Inverse:
Tripping Time: 0.07506 (S)

Highly recommended for practice engineers and electrical control/ operations engineering staff
Nice explained
Thanks